Skew heap
A skew heap (or self-adjusting heap) is a heap data structure implemented as a binary tree. Skew heaps are advantageous because of their ability to merge more quickly than binary heaps. In contrast with binary heaps, there are no structural constraints, so there is no guarantee that the height of the tree is logarithmic. Only two conditions must be satisfied:
- The general heap order must be enforced
- Every operation (add, remove_min, merge) on two skew heaps must be done using a special skew heap merge.
A skew heap is a self-adjusting form of a leftist heap which attempts to maintain balance by unconditionally swapping all nodes in the merge path when merging two heaps. (The merge operation is also used when adding and removing values.)
With no structural constraints, it may seem that a skew heap would be horribly inefficient. However, amortized complexity analysis can be used to demonstrate that all operations on a skew heap can be done in O(log n).[1]
Contents |
Definition
Skew heaps may be described with the following recursive definition:
- A heap with only one element is a skew heap.
- The result of skew merging two skew heaps
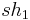 and
and 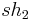 is also a skew heap.
is also a skew heap.
Operations
Merging two heaps
When two skew heaps are to be merged together, we can use a similar process as the merge of two leftist heaps:
- Compare roots of two heaps; let p be the heap with the smaller root, and q be the other heap. Let r be the name of the resulting new heap.
- Let the root of r be the root of p (the smaller root), and let r's right subtree be p's left subtree.
- Now, compute r's left subtree by recursively merging p's right subtree with q.
Non-recursive merging
Alternatively, there is a non-recursive approach which is more wordy, and does require some sorting at the outset.
- Split each heap into subtrees by cutting every rightmost path. (From the root node, sever the right node and make the right child its own subtree.) This will result in a set of trees in which the root either only has a left child or no children at all.
- Sort the subtrees in ascending order based on the value of the root node of each subtree.
- While there are still multiple subtrees, iteratively recombine the last two (from right to left).
- If the root of the second-to-last subtree has a left child, swap it to be the right child.
- Link the root of the last subtree as the left child of the second-to-last subtree.
Adding values
Adding a value to a skew heap is like merging a tree with one node together with the original tree.
Removing values
Removing the first value in a heap can be accomplished by removing the root and merging the child subtrees.and child subtrees are the part of root.
Implementation
In many functional languages, skew heaps become extremely simple to implement. Here is a complete sample implementation in Haskell.
data SkewHeap a = Empty | Node a (SkewHeap a) (SkewHeap a) singleton :: Ord a => a -> SkewHeap a singleton x = Node x Empty Empty union :: Ord a => SkewHeap a -> SkewHeap a -> SkewHeap a Empty `union` t2 = t2 t1 `union` Empty = t1 t1@(Node x1 l1 r1) `union` t2@(Node x2 l2 r2) | x1 <= x2 = Node x1 (t2 `union` r1) l1 | otherwise = Node x2 (t1 `union` r2) l2 insert :: Ord a => a -> SkewHeap a -> SkewHeap a insert x heap = singleton x `union` heap extractMin :: Ord a => SkewHeap a -> Maybe (a, SkewHeap a) extractMin Empty = Nothing extractMin (Node x l r) = Just (x, l `union` r)
References
- Sleator, Daniel Dominic; Tarjan, Robert Endre (1986). "Self-Adjusting Heaps". SIAM Journal on Computing 15 (1): 52–69. doi:10.1137/0215004. ISSN 0097-5397. http://www.cs.cmu.edu/~sleator/papers/Adjusting-Heaps.htm.
- CSE 4101 lecture notes, York University